La causa de la gravedad parece ser la tensión que soportan
dos campos, y los efectos son movimientos acelerados cuando no existen
restricciones que impidan los movimientos, pero el reposo relativo no impide
que los pesos manifiesten la presencia de una tensión. En la causa y en el
efecto existen fuerzas o acciones que se pueden igualar aunque sus raíces físicas
no sean las mismas. Si fueran las mismas, la aceleración debería ser una
propiedad de cada punto del espacio y no de los cuerpos, pero se hace difícil
creerlo, porque las cargas eléctricas en reposo también deberían emitir
radiación electromagnética, y no lo hacen.
Es muy extraño eso que llamamos masa de los cuerpos, podría
ser una cantidad de materia, o la relación entre su peso y el de otro que sirve
de referencia. Podría ser la relación entre dos caudales, o dos superficies.
Podría ser la relación entre magnitudes físicas cualesquiera, siempre que dicha
relación se mantenga invariable respecto del patrón de medida, que es un
cilindro metálico elegido de forma arbitraria. En ese cilindro también se
manifiesta un peso, y si la materia que vemos no es más que la proyección local
de campos que no vemos, en ese cilindro también existe un caudal, y tantas
superficies como las secciones en que pueda dividirse su corriente.
Cuando comparamos un cuerpo con ese cilindro patrón, ¿cuál
de todas esas magnitudes nos da una relación equivalente a su masa? La masa
puede ser cualquier magnitud que se derive de la forma en que interpretamos a
la materia, y las fuerzas pueden surgir de magnitudes diferentes, como por
ejemplo de una aceleración, pero también de una presión o de una tensión. Por
lo tanto, cuando determinamos una masa, la verdadera magnitud que medimos
dependerá del procedimiento de medida y de cómo interpretamos la realidad. De
todas las formas llegaremos al mismo resultado, pero los resultados iguales no demuestran
que las medidas correspondan al mismo tipo de magnitud física.
En el apartado 9 se ha interpretado el campo de una masa
como si fuera un sólido de masa y velocidad variables, llegando a la conclusión
de que las variaciones de masa deben compensar una aceleración tangencial que
no desaparece. Se entiende que este punto de vista corresponde al efecto
resultante de una acción central que representa la causa, y no puede
tener componente tangencial.
La causa queda definida por la ecuación 46 del apartado
anterior, pero su valor finito no basta para dinamizar una masa infinita.
Adicionalmente, el retardo de transporte no se ha tenido en cuenta ni en la
causa ni en el efecto. Estos dos problemas desaparecen si entendemos que un
campo está compuesto por infinitas secciones y que su masa localizada no es más
que una de las infinitas secciones, hasta la que se propaga la causa o acción
central. Por lo tanto, en cualquier instante, toda sección de la corriente
estará siendo afectada por una acción central que se propaga con velocidad
finita, y con retraso. Todo el conjunto de acciones retardadas que se aplican a
las infinitas secciones sí puede dar como resultado un valor infinito y
dinamizar el campo completo.
Por otra parte, si es cierto que los campos reaccionan y se
tensan, deberían comportarse como un sólido que amortigua los impulsos o
acciones que lo recorren, de forma que las acciones propagadas tendrían una
variación lineal entre la masa localizada y el campo central. Si la materia es
una realidad fluida y realimentada, las magnitudes físicas que se propagan
deberían tender a igualarse en cada intercambio de movimiento. De ser así, el
problema del retardo de transporte podría estar implícito en la distribución de
masa primitiva de los campos, y no sería necesario tenerlo en cuenta si
encontramos la distribución correcta.
Según el apartado 9, el efecto o consecuencia de la acción
central se puede obtener sustituyendo los resultados de las ecuaciones 43 y 45
en la ecuación 44 como indica el siguiente desarrollo, donde vemos que en la
ecuación 47 ya no existe la masa acumulada (m) ni su variación con el tiempo. Solo queda la distancia (r) al
centro de masas y la velocidad angular, además de sus derivadas, siendo Vr
la velocidad radial o primera derivada de la distancia, y siendo ar
la segunda derivada de la distancia.
La masa acumulada (m)
se puede obtener integrando la masa primitiva del campo como vemos a
continuación, cuyo resultado nos dice que es proporcional a la masa primitiva
asintótica m’0, que es una constante propia del campo y equivalente
a su caudal.
Eso significa que m’0 se puede incluir en la
constante de la ecuación 45, y la ecuación 47 se convierte entonces en la
siguiente, donde la constante pasa a ser la correspondiente a la unidad de masa
por quedar multiplicando a la masa m’0:
Se supone entonces que el resultado de la ecuación 49 es la
consecuencia de la acción central que indica la ecuación 46 del apartado
anterior, pero como dicha acción se propaga y se distribuye por todo el campo,
es necesario determinar de qué forma lo hace y cómo debe integrarse antes de
igualar su resultado con la ecuación 49, lo cuál no parece sencillo.
Si
lo aplicamos a una órbita circular, en la ecuación 49 se anula la velocidad
radial (Vr), la variación de la velocidad angular y la segunda
derivada de la distancia (ar). Además el producto r2ω
representa la velocidad areolar y será constante porque también lo será la
distancia y la velocidad angular. Por lo tanto no queda más que el producto de
la masa m’0, una constante, y la aceleración centrípeta -rω2.
Por
la otra parte, la acción que representa la ecuación 46 tiene que distribuirse
de forma constante por todo el campo, ya que si la órbita es circular no puede
variar la distancia ni el radio de enlace. Eso parece significar que la suma de
sus efectos sobre cada sección del campo debe ser una acción invariable por
cada elemento de masa acumulada, pero sacando factor común a dicha acción
invariable quedará la masa acumulada completa. Como la acción total debe ser
por unidad de masa para que se pueda multiplicar por cada incremento de masa
del campo, debe eliminarse m’0 de la acción central como vemos a
continuación, donde se iguala el efecto descrito en el párrafo anterior con la
causa que se acaba de comentar, en el caso de órbita circular.
Nótese
que el término m’0 siempre representa el campo completo, mientras
que el factor exponencial siempre representa a la unidad de masa porque su
valor es la unidad cuando la distancia r tiende a infinito. Por lo tanto, para
que la acción total de la ecuación 46 sea por unidad de masa, debe anularse m’0
y cambiarlo por el correspondiente incremento de masa en cada término del
sumatorio. En consecuencia, la masa m
y sus incrementos tendrían que ser masa primitiva (caudales) y no masa
acumulada del campo completo.
¿Debe
descartarse entonces el concepto de masa acumulada y cambiarlo por masa
primitiva? Enseguida trataremos ese problema, pero antes indicaremos que la ecuación
50 iguala dos magnitudes que no son equivalentes físicamente, por un lado densidad
o tensión del campo de mayor masa y por otra parte aceleración centrípeta. Es
completamente equivalente al modelo de gravedad que se trató en la segunda
parte, y aunque ya suene redundante, es equivalente a la gravedad de Newton en
el caso de una relación entre masas muy pequeña…
El radio de enlace (Re) sigue siendo el principal problema a
superar porque no está claro de qué forma se relaciona con la distancia y la
deformación de los campos. Si el concepto de masa acumulada es correcto (tal
como expresa la ecuación 48) y sabemos que debe ser una constante aunque varíe
la distancia, entonces el radio de enlace y la masa acumulada no deberían ser
proporcionales, ya que si lo fueran también debería ser constante el radio de
enlace. Eso es lo que vamos a comprobar definitivamente a fin de validar o
descartar el concepto de masa acumulada:
Definitivamente,
si anular la suma de términos tangenciales exige una masa acumulada constante,
entonces el radio de enlace también lo será, y eso parece ser incompatible con
una distancia variable. La ecuación 45 nos indica que debe ser constante el
producto mr2ω, pero no
necesariamente la masa m si se
admite alguna variación de la velocidad areolar r2ω. El problema es
que dicha variación tiene que ser muy pequeña, porque sabemos que las leyes de
Newton se cumplen casi a la perfección aunque no expliquen los efectos
relativistas. La masa podría ser variable, pero no lo suficiente para que el
radio de enlace cambie significativamente con la distancia.
Aunque las variaciones de masa sean muy pequeñas, las
ecuaciones 47 y 49 no se pueden descartar, pero sí podemos cuestionar otra vez
el concepto de masa. Efectivamente, la masa de los campos que se localiza en el
centro de masas carece de movimiento real, pero seguramente ha sido incorrecto
que sus proyecciones hacia posiciones localizadas deban tener solamente componente
real. Los campos están formados por hilos de corriente que fluyen en todo un
abanico de direcciones, desde radios pequeños hasta un radio infinito. Según la
relatividad ya es familiar considerar que la masa varía en la dirección del
movimiento, no es extraño entonces que cada hilo de corriente de un campo
aumente su proyección real si disminuye su radio de conexión con el campo
central, es decir, si aumenta el ángulo alfa según la figura.
Aunque
la masa acumulada por un campo no pueda ser casi constante, sí podría serlo la
proyección real, y eso significa que el radio de enlace (Re) debería ser el que
resultaría de hacer constante a la proyección real de la masa. Cuando la
distancia o deformación d aumente, los ángulos alfa del abanico de corrientes
aumentarán, y con ello las proyecciones reales de sus masas. Si aumenta entonces
el radio de enlace se incrementarán las proyecciones imaginarias, disminuirá la
densidad de las corrientes del campo, y las reacciones (más pequeñas) se
proyectarán en menor proporción en la dirección real de la deformación del
campo. Nótese que la deformación d es la misma para todos los hilos de
corriente y se puede considerar como proyección real de una distancia, pero no
de las reacciones que definen la “masa”. Aumentando Re, las corrientes apuntan
más en la dirección imaginaria, pierden densidad y pierden capacidad de reacción
en la dirección real.
De la ecuación de la masa primitiva (m’) se puede despejar
el radio r que corresponde a un valor cualquiera de m’. Para ese radio, un hilo
de corriente infinitesimal (dm’) se despegará del campo central formando un
ángulo alfa, pero la reacción del hilo en la dirección de la deformación ya no
será equivalente a la corriente dm’ sino a dm.
Sustituyendo la expresión de r en la otra expresión
recuadrada, se puede integrar el resultado para obtener completa la proyección
real de todo el caudal m’, desde cero hasta el valor asintótico m’0.
Nótese en el siguiente desarrollo que la relación d/Re es muy pequeña y se
desprecia.
Nótese igualmente que se ha cambiado el signo negativo del
resultado porque procede del cuadrado de un logaritmo neperiano, que siempre
será positivo.
La conclusión es
evidente: La única forma de que se mantenga constante la masa primitiva en
proyección real (m), es obligando al radio de enlace (Re) a ser proporcional a
la deformación del campo (d), y la causa que puede imponer dicha obligación es
que debe anularse la suma de acciones tangenciales, ya que no pueden ser
originadas por el campo central.
Insistimos una vez más en que hablar de masa es demasiado
subjetivo, pero sabemos que guarda una relación directa con las reacciones que
resultan de aplicar acciones externas. Como dichas acciones tienen la dirección
real en que se deforma el campo, es necesario proyectar las reacciones en esa
dirección, reacciones de una masa primitiva que como sabemos es un caudal.
Si la conclusión es correcta, el radio de enlace queda determinado
de forma definitiva, validando el modelo de gravedad propuesto en la segunda
parte. Sin embargo, un retardo de transporte implica un pequeño retraso del
radio de enlace respecto de la deformación del campo, lo que implica una masa
en proyección real que ya no será exactamente constante cuando varía la
distancia. Esa pequeña variación de la masa debe ser compensada con otra
pequeña variación de la velocidad areolar, pero el producto de masa y velocidad
areolar será constante como expresa la ecuación 45.
Es importante reconocer que la masa en el desarrollo
anterior es masa primitiva (caudal), y no masa acumulada. De haber sido masa
acumulada, tendríamos que haber multiplicado por la deformación d a cada hilo
de corriente, y hubiera resultado un radio de enlace proporcional al cuadrado
de la deformación del campo. Como el radio de enlace ya está elevado al
cuadrado en la acción del campo central según la ecuación 46, la gravedad
resultaría inversamente proporcional a la cuarta potencia de la distancia, que
es inaceptable.
No se puede considerar masa acumulada sino masa primitiva,
caudal que reacciona en mayor medida cuanto más frontal sea su impacto, y su
reacción en dirección real tiende a ser constante y máximo, tal como se observa
en la gráfica del desarrollo anterior. De ser así, dos campos que interaccionan
por gravedad estarán optimizando permanentemente su capacidad de reacción.
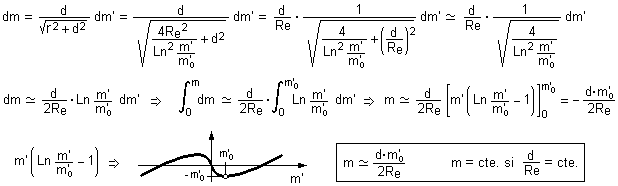
No hay comentarios:
Publicar un comentario