El origen de la relatividad especial de Einstein tiene
raíces profundas en una historia de referencias mal formuladas. Sin ellas no se
comprende la realidad que nos rodea y es inevitable que condicionen fuertemente
a la filosofía, a la religión y a la ciencia. Han cambiado mucho a lo largo de
la historia y probablemente lo seguirán haciendo, son arietes que destruyen
tradiciones, teorías y creencias. Todo lo que defendemos como verdad se
desmorona cada vez que profundizamos en la medida de las cosas, porque acabamos
perdiendo las viejas referencias.
Copérnico
dedujo en el siglo XVI que la Tierra no permanecía en reposo en el centro del
Universo, pero su trabajo no se publicó hasta el siglo XIX a pesar de que
explicaba los cambios en el Sol y las estrellas. Evidentemente, el Sol es una
referencia mucho mejor que la Tierra porque explica los retrocesos aparentes de
los planetas cuando los vemos desde la Tierra. El complicadísimo sistema de
epiciclos debió de provocar verdaderos dolores de cabeza a los antiguos
astrónomos.Gracias al telescopio, Galileo puede observar en 1610 la existencia de satélites orbitando a Júpiter, esperando demostrar que todos los cuerpos celestes no giraban alrededor de la Tierra. Según palabras del jesuita Cristóbal Clavio, Galileo aportó justificaciones más que suficientes para desmontar todo el sistema de los cielos, debiendo ser arreglado. Una de tales justificaciones fue la observación de las fases de Venus y una variación de su tamaño, solo compatible con la posibilidad de que girase alrededor del Sol. Lógicamente, si Venus orbitaba al sol también la Tierra lo haría, probablemente. El resto de la historia de Galileo ya se supone…, la teoría copernicana es condenada como insensata y herética.
El mismo Galileo establece como principio que es imposible
distinguir si un sistema está en reposo o se mueve con velocidad constante, ya
que no se puede fijar ninguna referencia como absoluta. Si un cuerpo se mueve con
velocidad constante respecto de un sistema de referencia, ¿cómo se sabe que no
es el sistema de referencia lo que se mueve? Este principio de relatividad de
Galileo se aplicaba solamente a los objetos y no al medio de propagación de la
luz, al que por entonces se llamaba éter y se imaginaba en reposo absoluto.
Como la Tierra se movería respecto del éter y la luz se propagaría en el éter
con velocidad constante, la velocidad de la luz respecto de la Tierra tendría
que ser diferente dependiendo de la dirección de medida. Si se moviera en la
misma dirección y sentido que la luz, la medida de la velocidad de la luz
tendría que ser menor de 300000Km/s, y sería mayor si la Tierra se moviera en
sentido contrario que la luz. La diferencia de velocidades tendría que ser la
velocidad absoluta de la Tierra. Así fue hasta principios del siglo XX cuando
Einstein era todavía un físico desconocido.
 ¿Y qué es la luz? Newton consideraba que estaba
compuesta por minúsculas partículas, pero el experimento de Young demostraba
que se comportaba como una onda cuando se hacía pasar a través de rendijas, ya
que dejaba claramente un patrón de interferencias que es típico de las ondas.
En 1905 Einstein publica su interpretación del efecto fotoeléctrico devolviendo
la razón a Newton, o al menos en parte, porque demuestra que existen cantidades
de luz indivisibles pero también es evidente su comportamiento como ondas por
el experimento de Young. No obstante, era tal la creencia en la naturaleza
ondulatoria que los físicos de la época se negaban a reconocer la cuantización
de la luz.
¿Y qué es la luz? Newton consideraba que estaba
compuesta por minúsculas partículas, pero el experimento de Young demostraba
que se comportaba como una onda cuando se hacía pasar a través de rendijas, ya
que dejaba claramente un patrón de interferencias que es típico de las ondas.
En 1905 Einstein publica su interpretación del efecto fotoeléctrico devolviendo
la razón a Newton, o al menos en parte, porque demuestra que existen cantidades
de luz indivisibles pero también es evidente su comportamiento como ondas por
el experimento de Young. No obstante, era tal la creencia en la naturaleza
ondulatoria que los físicos de la época se negaban a reconocer la cuantización
de la luz.
Robert
Millikan era por entonces uno de los físicos más reconocidos, especialmente por
el experimento que le permitió medir la carga eléctrica del electrón. No solo
fue responsable de bloquear la interpretación de Einstein durante 10 años sino
que pasó esos años intentando demostrar que era falsa, pero terminó demostrando
que era correcta por vía experimental. Einstein recibió el premio novel en 1921
por su demostración teórica del efecto fotoeléctrico, y Millikan lo recibió en
1923 por su demostración experimental.
 Lejos de aclarar cuál puede ser la naturaleza de la
luz, los experimentos aportan información pero convierten el problema en un
rompecabezas, en el que no sabemos si se propaga una onda, una partícula, las
dos cosas o ninguna. A pesar de todo, la luz es la referencia más universal que
se conoce y es imposible hablar de relatividad especial sin pensar en un rayo
de luz, así que lo tenemos que imaginar como algo inmaterial que se propaga en
el vacío a casi 300000Km/s, aunque solo se trate de una analogía que no
concuerda con la realidad.
Lejos de aclarar cuál puede ser la naturaleza de la
luz, los experimentos aportan información pero convierten el problema en un
rompecabezas, en el que no sabemos si se propaga una onda, una partícula, las
dos cosas o ninguna. A pesar de todo, la luz es la referencia más universal que
se conoce y es imposible hablar de relatividad especial sin pensar en un rayo
de luz, así que lo tenemos que imaginar como algo inmaterial que se propaga en
el vacío a casi 300000Km/s, aunque solo se trate de una analogía que no
concuerda con la realidad.
En el contexto del experimento de Michelson-Morley,
la luz era fundamentalmente onda y como tal necesitaba un medio de propagación
que no podía ser aire ni cualquier otro medio material conocido, pues era
evidente que la luz del Sol llegaba a la Tierra a través del vacío. Se
necesitaba un medio de propagación extraño que debería llenar el inmenso vacío
del Universo, al que se llamó éter.
Se dice con frecuencia que la velocidad de la luz es la
misma en cualquier dirección en la que se mida, y se atribuye esta conclusión al
experimento de Michelson-Morley, pero la verdadera evidencia es que no se
detectaron interferencias y el resto son interpretaciones.
Un interferómetro no mide la velocidad de la luz, solo
confirma o niega que dos haces de luz tardan el mismo tiempo en ser detectados,
pero si desconocemos qué se propaga y cómo lo hace ya no es tan evidente que la
luz se propague con igual velocidad en todas las direcciones. La condición de
un éter de propagación y la teoría electromagnética que la luz también cumple,
fueron las premisas que justificaron la misma velocidad de la luz en todas las
direcciones cuando se comprobó que no aparecieron interferencias.
Lo cierto es que los resultados del experimento negaban la
posibilidad de medir la velocidad de la Tierra respecto del éter, ya que Tierra
y éter tendrían que correr juntos con la misma velocidad. Si no había un éter
en reposo absoluto tampoco había referencia para medir velocidades absolutas…
¿o sí? Todavía era posible en el caso de que las distancias encogieran en la
dirección del movimiento, así de cruda era la suposición de Lorentz pero acabó
demostrando que era posible. No podía medir la contracción de las distancias
pero dedujo que de ser cierto los electrones tendrían que aumentar su masa, y
eso se ha verificado con tubos de rayos catódicos y aceleradores de partículas,
en concordancia con las deducciones de Lorentz, quien dedujo las
transformaciones necesarias para mantener la coherencia de las ecuaciones de
Maxwell, que son el fundamento del electromagnetismo.
Pero el éter tendría
que ser un medio de propagación muy raro como ya se explicaba en el experimento
de Michelson-Morley, tan raro que si una nueva teoría podía explicar el
experimento sin postular la existencia del éter sería reconocida de inmediato.
Y esa nueva teoría se la debemos a Einstein con su relatividad especial.
Los dos postulados de la relatividad
especial.
1.- Todos los sistemas de referencia inerciales deben ser
equivalentes. Esto
no significa que las medidas tengan que ser las mismas desde cualquier sistema
de referencia inercial, pero sí debe existir una transformación que permita
llegar a las mismas conclusiones. Se consideran sistemas inerciales aquellos
que permanecen en reposo o se mueven con velocidad constante.
2.- La velocidad de la luz es la misma constante para todos
los observadores. Esta
premisa es la condición que le sirvió a Einstein para deducir la transformación
de medidas entre dos sistemas inerciales, dando como resultado las mismas
transformaciones que Lorentz había obtenido en base al éter y la contracción de
las distancias. Por esta razón siguen conociéndose como transformaciones de
Lorentz aunque sea diferente su deducción y significado.
Las transformaciones de Lorentz contienen la esencia de la
relatividad especial y llevan implícitas todas las consecuencias. Se puede
pensar entonces que Einstein recibió un reconocimiento inmerecido, pero la
historia se lo atribuye supuestamente por una interpretación más profunda de la
realidad: El espacio y el tiempo dejan de ser independientes y no se necesita
postular ningún éter de características extrañas. Por otra parte, si las
transformaciones de Lorentz se deducen con la sola constancia de la velocidad
de la luz, también es cierto que a partir de las transformaciones puede
deducirse la constancia de la velocidad de la luz, y Lorentz pudo haber sacado
las mismas conclusiones que Einstein.
Si pudiéramos perseguir a un rayo de luz casi con su misma
velocidad, no veríamos que se aleja de nosotros lentamente, ¿veríamos que se
aleja con la velocidad constante de casi 300000Km/s? Y si pudiéramos hacer lo
mismo pero en sentido contrario a la propagación del rayo de luz, ¿seguiríamos
viendo que se aleja de nosotros con la misma velocidad constante de casi
300000Km/s?
El segundo postulado debería justificar que es cierto lo que
se acaba de cuestionar en el párrafo anterior, pero es evidente que si lo
reconocemos caeremos inmediatamente en una contradicción, porque si nos movemos
en sentido contrario a la luz tendríamos que reconocer una velocidad relativa
mayor de 300000Km/s, a pesar de que la medida nos diera siempre la misma
constante. ¿Qué es entonces lo que no encaja?
Según Galileo, las velocidades deberían sumarse o restarse,
pero Einstein nos hubiera dicho que no tiene sentido sacar conclusiones
anticipadas basándonos en la relatividad de Galileo, por ser incompatible con
la relatividad especial. Muy bien, esto significa que si queremos continuar no
debemos hacer caso de las contradicciones que se nos ocurran, puesto que son la
consecuencia de pensar en base a un principio que no es compatible con la
relatividad especial. Se puede decir de muchas formas, pero todas nos obligan a
practicar actos de fe poco elegantes para justificar contradicciones. Hagamos
ese acto de fe y avancemos en busca de conclusiones…
Relatividad en el tiempo.
 Supongamos que un observador lleva consigo un reloj
de luz como el representado en la figura, formado por dos espejos paralelos y
un fotón que se refleja en cada espejo, rebotando incansable y haciendo “tic”
cada vez que alcanza el espejo superior. Si el observador se mueve como se
indica en el segundo caso de la figura, el fotón también se mueve con el reloj
y su recorrido entre espejo y espejo pasa a ser oblicuo. Como su recorrido se
ha incrementado pero el segundo postulado nos dice que siempre tendrá la misma
velocidad constante, entonces el tiempo entre dos “tic” consecutivos habrá
aumentado. La conclusión es que el tiempo pasa más lento para cualquier cosa
que se mueve.
Supongamos que un observador lleva consigo un reloj
de luz como el representado en la figura, formado por dos espejos paralelos y
un fotón que se refleja en cada espejo, rebotando incansable y haciendo “tic”
cada vez que alcanza el espejo superior. Si el observador se mueve como se
indica en el segundo caso de la figura, el fotón también se mueve con el reloj
y su recorrido entre espejo y espejo pasa a ser oblicuo. Como su recorrido se
ha incrementado pero el segundo postulado nos dice que siempre tendrá la misma
velocidad constante, entonces el tiempo entre dos “tic” consecutivos habrá
aumentado. La conclusión es que el tiempo pasa más lento para cualquier cosa
que se mueve.Las interacciones entre partículas debemos entender que ocurren a la velocidad de la luz, por lo que no hay actividad que se salga de la norma. Todos los relojes, toda actividad biológica y en general todo lo que experimenta cambios, tiene que ser afectado de la misma forma y experimentar un tiempo que se hace más y más lento cuanto mayor sea la velocidad.
¿Y qué pasaría si cambiamos la orientación del reloj? Pues que su “tic” y su “tac” ya no correrían con la misma rapidez. No solo el tiempo, también masa y distancia son afectados de forma distinta según la dirección en que se miden, pero no vamos a profundizar en ello.
Pero se ha dicho que la velocidad es relativa y no se puede saber si algo se mueve o es la referencia lo que se mueve. Un observador considerado en reposo (relativo por supuesto) verá que el tiempo pasa más despacio para otro observador en movimiento. Sin embargo el que suponemos en movimiento entenderá que es él quien está quieto y que es el otro el que se mueve. Por lo tanto los dos observadores verán que el reloj del otro atrasa. Cada uno ve las cosas desde su propio sistema de referencia pero las transformaciones de Lorentz las hacen equivalentes.
La siguiente ecuación expresa la relación entre los tiempos que medirían dos observadores inerciales. Los dos calcularían su propio tiempo como “T” porque verían que es el otro quien se mueve, y entenderían que “Tr” es el tiempo del otro. Se entiende que si la velocidad “v” se aproximara a la velocidad de la luz “c”, entonces para un determinado tiempo T resultará que Tr se aproxima a cero. En concreto, el tiempo que pasaría para un fotón será siempre cero porque su velocidad coincidiría con c, por ese motivo se dice que los fotones mantienen su estado cuántico, como si estuvieran congelados en el tiempo.
El problema de la simultaneidad.
 Supongamos un observador dentro de una cámara con una
bombilla en el centro y espejos en las paredes. Cuando enciende la bombilla verá
el reflejo en cada pared al mismo tiempo, entendiendo que los dos sucesos han
ocurrido a la vez. Al contrario, para un observador exterior que ve moverse a
la cámara, una de las paredes estará acercándose hacia la luz y será alcanzada
por un rayo antes que la otra pared, puesto que la luz tendrá recorridos
diferentes. La velocidad de la luz tiene que ser la misma para los dos
observadores, de forma que para el exterior uno de los rayos tardará menos
tiempo en llegar al espejo porque se lo encuentra más cerca. Es claro entonces
que lo simultáneo para un observador no lo es para otro.
Supongamos un observador dentro de una cámara con una
bombilla en el centro y espejos en las paredes. Cuando enciende la bombilla verá
el reflejo en cada pared al mismo tiempo, entendiendo que los dos sucesos han
ocurrido a la vez. Al contrario, para un observador exterior que ve moverse a
la cámara, una de las paredes estará acercándose hacia la luz y será alcanzada
por un rayo antes que la otra pared, puesto que la luz tendrá recorridos
diferentes. La velocidad de la luz tiene que ser la misma para los dos
observadores, de forma que para el exterior uno de los rayos tardará menos
tiempo en llegar al espejo porque se lo encuentra más cerca. Es claro entonces
que lo simultáneo para un observador no lo es para otro.
Una causa y su efecto también serán sucesos, y nos podemos
preguntar si el efecto pudiera ser visto antes que la causa por un observador determinado.
La respuesta es que la causa y su efecto pueden acercarse o alejarse en el
tiempo, pero la causa siempre ocurre primero para todos los observadores. Por
ejemplo, el instante en el que se enciende la bombilla en el ejemplo anterior
siempre se verá antes que cualquiera de los reflejos en las paredes.
La contracción de las distancias.
Si nos fijamos en la pared izquierda del ejemplo anterior, vemos
que la luz tardará menos tiempo en alcanzarla porque la pared se le acerca. Un observador
externo vería la distancia contraída porque la luz tardaría menos tiempo pero
la velocidad de la luz es invariable. Al contrario, si nos fijamos en la pared
derecha las cosas cambian porque la distancia se vería dilatada.
Tal como se ha explicado con la relatividad en el tiempo, nada cambia para un fotón cuando recorre una distancia, es decir, el tiempo no corre para él pero sí corre para un observador externo. La única forma de hacerlo compatible es que la distancia para el fotón sea cero. Cuanto mayor sea la velocidad más cortas parecerán las distancias.
Tal como se ha explicado con la relatividad en el tiempo, nada cambia para un fotón cuando recorre una distancia, es decir, el tiempo no corre para él pero sí corre para un observador externo. La única forma de hacerlo compatible es que la distancia para el fotón sea cero. Cuanto mayor sea la velocidad más cortas parecerán las distancias.
Relatividad en la masa.
Supongamos que un lanzador impulsa una bola de masa
M1 con una velocidad V1, siendo entonces la cantidad de movimiento igual al
producto M1·V1. Siendo v la velocidad relativa respecto de otro observador, éste
último tendría diferente perspectiva porque vería correr más despacio el tiempo
del lanzador, impulsando la bola lentamente y por lo tanto con una velocidad V2
más pequeña.Si la cantidad de movimiento debe ser la misma desde los dos puntos de vista, entonces debe cumplirse que M1·V1 = M2·V2, y como V2 tiene que ser menor que V1 como se ha dicho en el párrafo anterior, entonces el segundo observador notaría una masa M2 más grande.

Las velocidades no se suman.
 Si un primer objeto se mueve con velocidad v y otro segundo objeto se mueve
respecto del primero con velocidad w,
la velocidad del segundo sería según la mecánica clásica W = v + w. Esto no es así en relatividad especial, y lo mismo que
sucede con otras magnitudes relativas, las transformaciones de Lorentz también
explican lo que pasa cuando se plantea una suma de velocidades.
Si un primer objeto se mueve con velocidad v y otro segundo objeto se mueve
respecto del primero con velocidad w,
la velocidad del segundo sería según la mecánica clásica W = v + w. Esto no es así en relatividad especial, y lo mismo que
sucede con otras magnitudes relativas, las transformaciones de Lorentz también
explican lo que pasa cuando se plantea una suma de velocidades.En el caso límite en el que las dos velocidades llegaran a ser iguales a c (velocidad de la luz), entonces el denominador se hace igual a 2, y la velocidad resultante sería igual a c, por lo que no es posible rebasar la velocidad de la luz.
Experimento de Fizeau.
El propósito inicial era distinguir si el medio de propagación
de la luz (éter) era arrastrado por la materia o si por el contrario se mantenía
estático, ya que si recordamos el experimento de Michelson-Morley no había sido
decisivo. Sin relatividad tenía que ser arrastrado, pero si era cierta la
contracción de las distancias tenía que ser estático.
 Un haz de luz se divide en dos recorridos, el 1 se propaga
en contracorriente sobre agua en circulación, y el 2 lo hace a favor de la
corriente. Si el éter fuera estático no importaría si el agua se mantiene en
reposo o circula con una velocidad “v”, por lo que no deberían detectarse
interferencias entre los dos haces. Si el éter fuera completamente arrastrado,
la velocidad del agua debería restarse en el tramo 1 y debería sumarse en el
tramo 2.
Un haz de luz se divide en dos recorridos, el 1 se propaga
en contracorriente sobre agua en circulación, y el 2 lo hace a favor de la
corriente. Si el éter fuera estático no importaría si el agua se mantiene en
reposo o circula con una velocidad “v”, por lo que no deberían detectarse
interferencias entre los dos haces. Si el éter fuera completamente arrastrado,
la velocidad del agua debería restarse en el tramo 1 y debería sumarse en el
tramo 2.
Siendo “n” el índice de refracción de un medio material como
el agua, la velocidad de la luz en ese medio en reposo es c/n, y en el caso de
un éter totalmente arrastrado las velocidades deberían ser:
La conclusión del experimento fue que había interferencias y el éter no podía ser estático, pero las velocidades esperadas en el caso de un éter completamente arrastrado tampoco coincidían, ya que las diferencias de tiempos resultaron aproximadamente un 43,5% de lo esperado. Independientemente del fluido utilizado, los desfases obtenidos estaban bastante ajustados con las velocidades experimentales que se indican a continuación, y la conclusión era un éter parcialmente arrastrado por la materia.
C1 = c/n –
v y C2 = c/n + v
La conclusión del experimento fue que había interferencias y el éter no podía ser estático, pero las velocidades esperadas en el caso de un éter completamente arrastrado tampoco coincidían, ya que las diferencias de tiempos resultaron aproximadamente un 43,5% de lo esperado. Independientemente del fluido utilizado, los desfases obtenidos estaban bastante ajustados con las velocidades experimentales que se indican a continuación, y la conclusión era un éter parcialmente arrastrado por la materia.
Ya sabemos que la relatividad especial puso fin a la teoría
del éter, y naturalmente puede justificar velocidades bastante ajustadas a las
anteriores cuando la velocidad (v) del medio material es muy pequeña comparada
con la de la luz. En la ecuación de adición de velocidades que se ha visto
anteriormente se puede sustituir w por c/n, como velocidad de la luz respecto
del medio en reposo, y desarrollando y teniendo en cuenta que v << c, se llega
a las mismas velocidades que se habían obtenido experimentalmente. Como es lógico,
a medida que v se acerca a la velocidad de la luz, la ecuación de adición de
velocidades arroja valores para C1 y C2 que también se
acercan a la velocidad de la luz, pero nunca la rebasan.
Si recordamos que la fórmula de adición de velocidades ha
sido deducida de las transformaciones de Lorentz, entonces parece haber algo
contradictorio. Por una parte, Lorentz justificaba un éter estático basándose
en la contracción de la distancia, y necesitó añadir sus transformaciones para
mantener la coherencia de las ecuaciones de Maxwell. Sin embargo, esas mismas
transformaciones nos conducen a la fórmula de adición de velocidades, apoyan a
un éter parcialmente arrastrado y no estático. Incluso dejando de lado la teoría
del éter, no se puede olvidar que la relatividad de Lorentz y la de Einstein
son equivalentes matemáticamente, y por lo tanto se debería considerar absoluta
la velocidad de la luz, como si la nada en la que supuestamente se propaga
fuera tan estática como el éter de Lorentz. Pero si la nada es estática, no
puede ser a la vez arrastrada parcialmente por la materia.

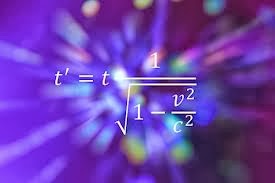




En el problema de la simultaneidad se convierte en problema porque se deshecha el medio de propagación. Siempre que hay movimiento, al especificarlo solo con respecto a otro observador pero no distinguir si se hallan en el mismo medio o en otro medio diferente, todo termina en la nada dogmática.
ResponderEliminarMuy interesante lo de Fizeau. Algo que caracteriza al medio material transparente, como el agua, del medio donde se propaga la luz en el vacío, es que n no solo desvía un rayo de luz y hace que viaje más despacio, sino que por un lado el material absorbe energía y por el otro el valor de n depende de la frecuencia del haz, algo que no ocurre, o bien, si ocurre no es detectable, en el vacío. Para frecuencias elevadas, como los rayos X, n es menor a 1, desviando el haz en otra dirección y haciendo a cn ligeramente mayor a c.
Saludos Edgardo. ¿Seguro que el índice de refracción (n) depende de la frecuencia de la luz? Hace mucho que no consulto nada sobre relatividad porque en todas partes encuentro lo mismo y termina aburriendo, pero siempre pensé que n solo dependía del medio, habrá que volver a releer algunas cosas. También me cae de sorpresa que n pueda ser menor de 1 con rayos X, haciendo que c/n sea mayor a c.
EliminarHola Jesús. Seguro, y no tiene que ver con relatividad sino con física óptica. Cuando se dice que el agua tiene un valor n de 1,333, ese valor se corresponde a una fuente de luz monocromática de sodio. También depende de la temperatura y la presión, pues se dan esos otros valores en la tabla de índices de refracción. Asimismo, que el ángulo de desviación depende de la frecuencia es lo que resulta en la llamada dispersión de la luz compuesta de muchos colores, y a su vez distintas sustancias refractivas pueden hacer que la banda de colores resulte de distinta anchura. El efecto de dispersión causa distorsión o pérdida de datos en fibras ópticas debido a que distintas longitudes de onda viajan a velocidades diferentes, deformando el paquete de ondas. Con relación a los rayos X hay información que indica que el valor de n es menor a 1 para sustancias cuyo valor es mayor a 1 para ondas lumínicas. Y aquí surgen discusiones relativistas.
ResponderEliminarTienes toda la razón, en el tema de óptica estoy muy verde porque ni me había preocupado por qué se formaba toda la gama de colores, y evidentemente debe ser porque el índice de refracción depende de las frecuencias. Todavía no tengo claro por qué se forma el arco iris cuando la luz del sol se refracta en las gotas de lluvia.
Eliminar